EMISSION

LA CHAINE SONORE

I - L'émission

a. Les instruments musicaux : des émetteurs

Dans un premier temps, nous allons donc étudiez l'émission du son par les instruments musicaux. Ceux-ci se classent en trois catégories :
- les instruments à vent (flûte, clarinette)
- les instruments à cordes (guitare, violon)
- les instruments à percussion (timbales, xylophone)
Pour mieux comprendre le mécanisme, nous utiliserons la guitare qui sera notre principal exemple étant donné que tous les instruments fonctionnent de la même manière pour produire des sons.

Comment les instruments de musique produisent-ils un son ?

Emission sonore et vibration

Pour produire un son, les instruments de musique doivent remplir deux fonctions : vibrer et émettre.
Ils comportent un système mécanique vibrant : l’excitateur (corde, sifflet ou anche), accompagné d’un résonateur (l’air d’une caisse ou d’un tube) qu’il met en oscillation forcée : mouvement de va-et-vient de part et d'autre d'une position d'équilibre. En effet, un guitariste pince les cordes de sa guitare pour provoquer la vibration d’une partie de l’instrument. Ceci va être couplé au résonateur : la caisse de la guitare va amplifier le son. Ainsi, le système mécanique produit l’onde sonore avec une intensité suffisante pour qu’elle soit audible.
Un son correspond donc à une onde sonore, vibration longitudinale des tranches d’air qui se transmet de proche en proche. Emettre un son, c’est mettre en mouvement des tranches d’air qui vont propager l’information sous forme d’ondes sonores. Le mouvement de ces tranches d’air s’effectue par vibrations d’une partie mobile immergée dans l’air (ou dans le fluide dans lequel on émet l’onde).

Sur la photographie ci-contre, on observe les vibrations émises par les cordes d'une guitare mises en mouvement : les vibrations sont à la base du son. Puis ces vibrations sont associés à un résonateur qui est ici la caisse de la guitare. Son mécanisme est simple : dans le corps creux, l’onde sonore rebondit contre les parois faisant vibrer le bois, et lorsqu’une onde entre dans cette chambre remplie d’air, elle ne cesse de rebondir contre les parois augmentant à chaque fois la vibration du son. C’est la caisse de la guitare qui donne toute son ampleur à la note. Le son est ainsi entendu.

Photographie représentative des vibrations de la caisse de la guitare lors de l’émission d’un son.

Le système vibrant

Nous allons maintenant étudier plus précisément le système vibrant pour comprendre comment vibre une corde tendue entre deux points fixes.

→ Le système mécanique vibrant

Les cordes d’une guitare sont tendues parallèlement au manche. Lorsqu’une corde vibre dans toute sa longueur, elle oscille et crée une onde progressive. La superposition de deux ondes progressives d’amplitude égale et se propageant en sens contraire est appelée onde stationnaire.

Le mot stationnaire peut trouver sa justification dans l’observation suivante : l’onde progressive qui se propage vers la gauche emporte une certaine quantité d’énergie vers la gauche, réciproquement l’onde progressive qui se déplace vers la droite (et qui a des caractéristiques identiques) emporte la même quantité d’énergie vers la droite ; en conséquence il n’y a pas de transport net d’énergie, d’où l’appellation d’onde stationnaire.

→ Le système mécanique vibrant

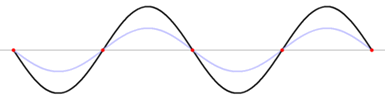
Pour certaines valeurs de fréquence appelées fréquences propres, la corde vibre avec une grande amplitude formant plusieurs fuseaux.
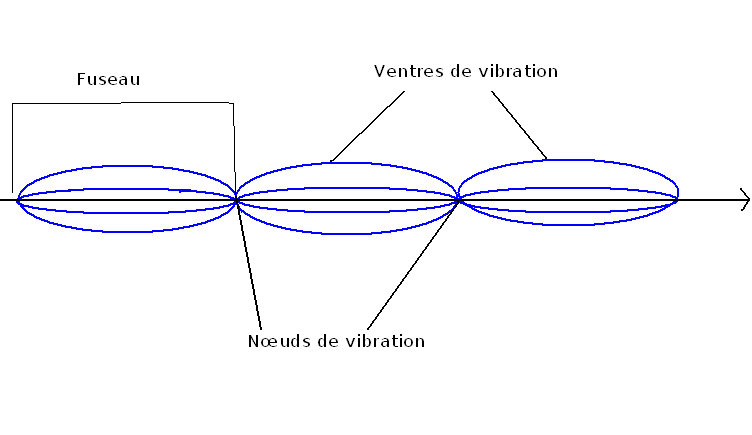
A la résonance on observe un certain nombre de fuseaux, qu’on note k, qui sont égaux et identiques. Les extrémités des fuseaux sont immobiles et d’amplitude équidistante : il s’agit des nœuds de vibration. Entre les nœuds se trouvent les points dont l’amplitude de vibration est maximale : ce sont les ventres de vibration. Il y a un nombre limité de modes de vibration possibles : c’est la quantification des modes propres de vibration d’une corde tendue.

→ Le système mécanique vibrant

Le mode fondamental pour lequel la corde vibre en seul fuseau de fréquence f0

Schéma d’une corde en vibration créant une fondamentale.

Les harmoniques pour lesquels la corde vibre en plusieurs fuseaux et qui correspond aux fréquences fk=k.f0. Pour l’harmonique k la longueur d’un fuseau est égale à L / k où L est la longueur de la corde.
Il s’agit par exemple de la guitare où la corde peut vibrer en plusieurs fuseaux séparés par plusieurs nœuds.

Schéma d’une corde en vibration contenant trois fuseaux.

→ Calcul de la fréquence d’une onde grâce à un fuseau :

L la longueur de la corde (mètre : m)
f la fréquence de l’onde (Hertz : Hz)
V sa vitesse, (mètre/seconde : m/s)

Pour un fuseau :    f0 = V/2L = (1/2)V/L
pour deux fuseaux          f1 = V/(2L/2) = V/L = 2f0
pour trois fuseaux          f2 = V/(2L/3) = (3/2)V/L = 3f0
pour quatre fuseaux        f3 = V/(2L/4) = 2V/L = 4f0
En conclusion, la fréquence d’onde d’un fuseau est calculable grâce à la formule :

fk/(k+1) (avec k entier)

Cette formule permet de calculer la vitesse de l’onde, la longueur de la corde ou la fréquence de l’onde qui crée le fuseau. F0 est donc la fréquence fondamentale, tandis que f1, f2, f3 , fk sont ses harmoniques.

→ Les cordes frappées ou pincées

Quand une corde est pincée, par exemple corde de guitare, ses oscillations sont libres. Elles produisent un son composé de sons sinusoïdaux (alternatifs) dont les fréquences sont des multiples de la fréquence du signal de départ. La fréquence du son produit est égale à la fréquence du mode fondamental f0.

Autre source sonore : colonne d'air

Il est également possible d’exciter des ondes en mettant en mouvement de l’air dans un tube : tuyau d’orgue, de flûte, de clarinette, etc. Le mécanisme est très similaire à celui des ondes excitées sur une corde tendue :
Comme pour la corde de guitare, ces fréquences sont les fréquences des modes de vibration de la colonne d’air : elles sont quantifiées. Si le mode fondamental a pour fréquence f0, les modes harmoniques ont pour fréquence fk=k.f0, où k est un entier.

La longueur du tuyau joue un grand rôle dans les fréquences. Les fréquences de résonance d’une colonne d’air de longueur L, sont quantifiées et leurs valeurs dépendent de la longueur. Plus le tuyau est court, plus la valeur de la fréquence du mode fondamental est élevée. Les sons aigus sont favorisés par des tuyaux courts et les sons graves par des tuyaux longs.

Page suivante